Nina Kolarzik

Walking through Malmö, you can hear a mix of different languages. The same counts for international congresses, parliaments, round tables, etc. Did you ever think about the information you miss out on because you do not understand the people’s native language. Of course there is the possibility of translation, but what if information and meaning gets lost on the way?

Lost in Translation – What does “I am Groot” mean?

Imagine you live in a country with a centuries-old arch enemy as your neighbour. There exists no open conflict, but they are not far away from that. Then, at a conference, diplomats exchange some highly sensitive sentences. It is a fine line to walk on because they want to appear strong, but not aggressive. The problem is that depending on the context, different translations exist for most words.

Thus, to a certain extent, there is always an interpretation that comes with the translation. What can happen is that one diplomat hears from his interpreter a translation, where a critique sounds more like an insult, intentionally or not. And suddenly the two countries are at war.

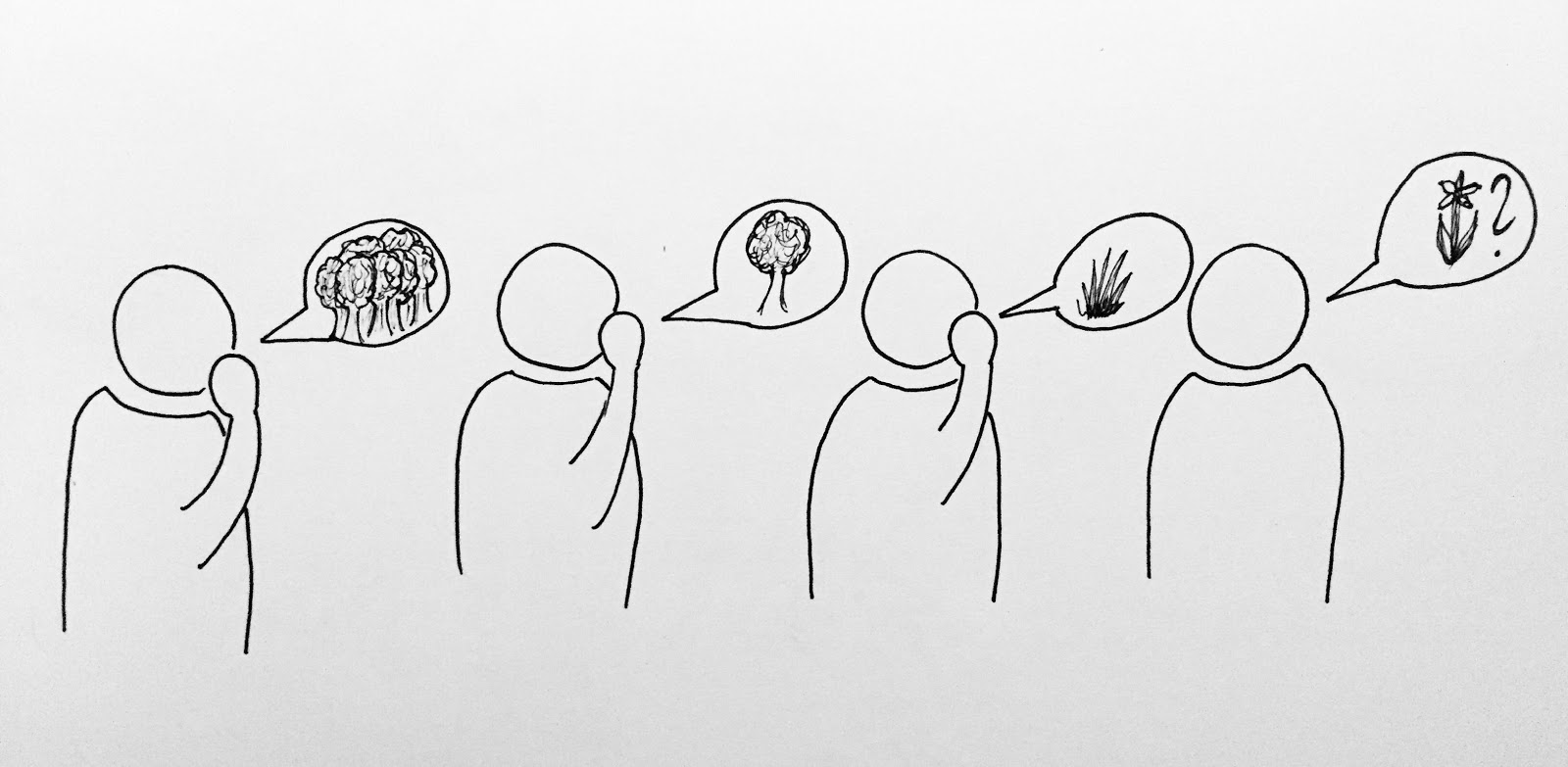
It sounds like an over-exaggerated script of a bad movie, but I can imagine it becoming reality. It shows the responsibility and power of translation. We all know of examples in the political history of the world, where few words had a significant impact. If you nail it down, words are the essence of politics. And since international politics takes place in dozens of different languages, one may wonder how much the differences between those languages matter. Some words cannot be exactly translated into other languages. Some meanings might be slightly different. Sometimes the translator might not understand the exact intention of the speaker.

Unnoticed, but Decisive

Because we all are simple human beings, mistakes may happen when translating. And just as a snowball can become an avalanche, one incorrect translation or transcription could make a big difference. For example, some historians argue that the slight changes Bismarck made when he gave the Ems Dispatch to the press were responsible for the outbreak of the Franco-Prussian War.

Usually, the translators and interpreters who work in high positions of politics are not really visible. Their work happens during and in between an international discussion or negotiation. Their task is to enable negotiations and not to record them. The task of translators and interpreters in government services is to equip diplomats with the ability to communicate, negotiate, as well as pass on information to all parts of the world. As an outsider you do not notice the huge significance their job has. But the significance is undeniable since in today’s world politics people with hundreds of different native tongues come together to communicate.

The difference between a translator and an interpreter in this context is, that a translator works with documents that they translate after they are produced, while an interpreter translates simultaneously during a negotiation, so that participants can follow a debate in real time.

Putin, Trump and the third person in the room

It was a politically remarkable meeting of the Presidents Putin and Trump in Helsinki in July this year. It was an unusual situation, that the two state leaders met for more than two hours without anyone else in the room. Usually, when there is a meeting on this level of importance, with this special relationship, there are always some other persons present: aides and official note takers, etc. This time, there were only the two state leaders and their translators in the room, which puts public attention and a level of importance on the translators that they may not have experienced before and triggered some debate about the value, responsibility and right of information.

Since Trump is not exactly known for giving out trustworthy information, many American politicians see the only chance to get reliable insights on what happened in the meeting in the US interpreter Marina Gross . US Congressionals requested her to testify concerning what the two state leaders were really talking about for hours. That caused a loud outcry and fierce debate about what the duties and the rights of translators are.

Tinker Tailor Translator Spy?

The whole community of translators and interpreters got worried about their status as an apolitical “extension of the principal”; somebody who is just there to give the possibility for the politicians to speak to each other as they would if they spoke the same language. Humaira Peroz, an International Relations student of MAU and UF Head Program Coordination, who works as a translator for Språkservice and Tolkresurs, explains the ethical code of the Swedish Kammarkollegiet she has to follow: “We basically have no individual presence during our working hours and are supposed to be a “tool” with no human reaction or emotions”. This ethical code includes that translators are: “‘bound by the strictest secrecy” when they are hired on a high political level, “which must be observed towards all persons and with regards to all information disclosed in the course of the practice of the profession at any gathering not open to the public’” (article 2 of the International Association of Conference Interpreters (AIIC) Code of Professional Ethics for interpreters in diplomatic roles). They compare themselves to doctors or priests, who also vow to treat the information they receive confidentially. Some call them “James Bonds of the linguistic world” to show their secretive importance.

If Marina Gross testifies it could be used as a precedence and no statesmen would ever use an interpreter at that level again, when they know that the confidential information they are dealing with could be revealed. That is what Republicans argue for. It is feared, that diplomacy in itself would be threatened. However, Democrats point out that the public has the right to know, what the meeting was truly about. So far the state department and the justice department protected translators in legal cases from having to testify. But it has also never happened before that in such a meeting no official note-taker was present which makes the situation new and difficult for everyone.

As the New York Times formulates it, the origin for the politicisation of the translator’s is the mistrust in President Trump. Eventually they were able to agree on at least revealing Gross’ notes from the meeting. Despite the ethical questions, the practical issue is that interpreters’ notes are taken for simultaneous translating and not for keeping record. They are taken in a personal shorthand for the short-term memory of translating something in the situation of the moment—they are useless for anyone else and interpreters often cannot make sense of their own notes later anymore. Their ethical code can limit translators “from taking actions in situations where you normally would take a stand”, says Humaira Peroz, “but while one is working it is difficult to know what’s appropriately right or wrong”.

So, what does “I am Groot” mean? – It’s up to you…

What do we conclude from that? That a big deal in world politics is about knowledge. About knowing the truth. That this is not an easy thing to figure out. Many of the stages, information goes through, we do not even see or notice. And we can barely reveal all the influences, that alters information before it reaches us. Think about the news, about when you cannot understand the original because the news interpreter talks over it: how does the image of a situation change through the translation people hear? How differently do we judge happenings depending on the amount and type of information we get? How differently do we understand things within a conversation, on the basis of our different native tongues. How much can meanings be altered through translations?

All these are questions we do not ask ourselves often but the issue has a bigger importance than we might think. So this is my message for you: question and trace back the information you get!

By Nina Kolarzik

Photo Credits

“Flags at the UN”, by http://www.worldislandinfo.com/ (CC BY 2.0)

“Language, Learning, Books” by Oli Lynch (CC0 1.0 Universal)